■ 외부적 표현 방식
code로 표시하여 사람이 이해할 수 있도록 표현한 방식이다. (비트 수 꼭 암기)
| 종류 | 설명 |
| BCD code (Binray Code Decimal) |
IBM에서 제작한 방식. 2진화 10진 코드로 불린다. 6비트로 구성되어있고 영소문자 사용이 안되며, 수치 계산용으로 사용된다. - Zonebit 2개, DigitBit 4개, (2^6 = 64가지 표현 가능)  |
ASCII Code (American Standard Code for Information Interchange) |
미국 표준 협회에서 개설. 7비트로 구성되어있고 보통 통신 제어용으로 사용되어지고 마이크로 컴퓨터 기본코드로 사용된다. - Zonebit 3개, DigitBit 4개, (2^7 = 128가지 표현 가능) 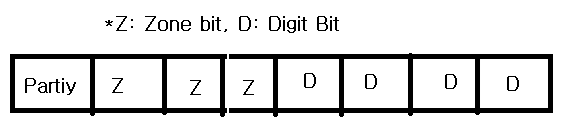 |
EBCDIC (Extended Binary Coded Decimal Interchange Code) |
IBM에서 제작한 방식. 확장 2진화 10진 코드로 불린다. 8비트로 구성되어있어 중대형 컴퓨터에서 사용된다. - Zonebit 4개, DigitBit 4개, (2^8 = 255가지 표현 가능)  |
| BAUDOT code (보도 부호) |
1개의 문자가 5개의 비트로 표현되는 정보 부호, ASCII Code가 출현할 때 까지 가장 많이 사용되었다. 5비트로 구성되어있어 32가지 표현이 가능했다. |
| * 패리티 비트 코드의 오류를 검사하기 위해서 데이터 비트 외에 추가한 1비트 데이터. 아래 자세한 설명 있음 * 존(Zone)비트와 숫자(digit)비트로 분리되는데 영문인지 숫자인지 구분하는 비트들임. |
|
| [ ▼ 기타 표현 방식 ] | |
| BCD Code (8421코드) |
위에 언급된 BCD code랑 다른 종류. 보통 8421 코드라고도함 - 10진수 1자리를 2진수 4자리(bit)로 표현하는 '가중치 코드' - 문자 코드인 BCD에서 Zone 부분 생략한 형태 - 10진수 입·출력이 편함 (가중치 코드란 우리가 1001 2진수를 계산할때 2^3, 2^2, 2^1, 2^0으로 곱해서 계산한다. 이런 가중치가 적용된 코드이다) (문제) 10진수 956를 BCD코드로 변환해라 = 9(1001) 5(0101) 6(0110) = 1001 0101 0110 |
| 해밍 코드 (★) (Hamming) |
- 오류 검출, 정정 가능 * 패리티 비트는 검출은 가능하나 정정이 불가능함 (공식) 최소 해밍거리 >= 2 X 정정 가능 오류 수 + 1 (문제) 전송하려는 부호어들의 최소 해밍 거리가 6일 때 수신 시 정정할 수 있는 최대 오류 수는? -> 5 >= 2 * 정정가능 오류 수 -> 2.5 >= 정정 가능 오류 수 -> 정정 가능 오류수는 정수이므로 최대값은 답 = 2 |
| 그레이코드 (Gray) |
- BCD 코드의 인접한 자리를 XOR연산으로 만든 코드 (비가중치 코드) - 이웃하는 코드가 한 비트만 다르기 때문에 코드 변환이 용이(이는 eroor를 최소화 해준다)해서 아날로그/디지털 변환, 데이터 전송에 주로 사용 2진수 : 1 0 0 1 그레이코드 : 1 1 0 1 (첫번째 자리는 그대로 내려오고 'ㄱ'자형태로 1 0의 XOR은 1이기 떄문에 1이 내려온다 세번째 숫자또한 0 XOR 0 은 0이기 때문에 0이내려온다) 여기서 2진수로 변환하면 그레이 코드 : 1 1 0 1 2진수 : 1 0 0 1 이 된다 그레이 코드 첫번째 숫자는 내려오고 2진수 첫번째 숫자와 그레이 코드 두번째 숫자 XOR해서 0이 2진수 두번째 숫자가 된다. 또 2진수 두번째 숫자와 그레이코드 세번째 숫자 XOR해서 2진수 세번째는 0이된다. 이런 식으로 ㄱ이 기울어진 형태로 계산하면됨  (문제) 2진수 0111을 그레이 코드로 변환하면? (답) 0100 |
| 패리티 검사 (Parity) |
- 오류 검출(O), 정정 (X) - 짝수 패리티, 홀수 패리티가 있다. - 송신 측에서 보내려는 데이터의 1의 개수가 홀수면 패리티 비트에 0을 짝수면 1을 넣어준다. 그래서 예를 들어 송신 측에서 패리티 비트에 [0]1011을 넣었는데 수신 측에서 [0]1001을 받으면 정상적으로 수신 받지 않았다는 것을 알 수 있다. * 짝수, 홀수인지만 판단하는 것이지 어디가 바뀌었는지는 알 수 없다. |
■ 내부적 표현 방식
1. 고정 소수점 표현
정수 데이터의 표현 및 연산에 사용하는 방법
| 종류 | 설명 |
| 2진 연산 | 부호비트 (0 -> 양수, 1 -> 음수) |
| 10진 연산 | (1) UnPack 형식 (Zone 형식) : 10진수 입 · 출력 - 1 Byte로 10진수 1자리 표현 - 마지막 바이트에 양수[음수]를 표기 한다. 양수 : C, 음수 : D - 나머지 바이트는 F로 표기 (ex) +123 은 |F1|F2|C3 F1, F2, C3 각각 1Byte로 표현한다.  (2) Pack 형식 : 10진수 연산 - 1 Byte로 10진수 2자리 표현 (ex) -2001 => 마지막에 D가 들어간다. 00000000에서 뒤로부터 작성해서 00|02|00|1D 즉 00 02 00 1D로 표현해준다. |
2. 부동 소수점 표현
실수 데이터의 표현과 연산에 사용되는 방법
- 고정 소수점 표현보다 표현의 정밀도를 높일 수 있다. (과학이나 공학 또는 수학적인 응용에 주로 사용)
- 고정 소수점 표현에 비해 연산이 복잡하므로 연산 시간이 오래 걸린다.
728x90
'자격증 및 시험 > 정보처리' 카테고리의 다른 글
| [컴퓨터] 명령어 처리 과정 (0) | 2023.05.01 |
|---|---|
| [컴퓨터] 컴퓨터 시스템 구성 (0) | 2023.05.01 |
| [전자계산] 자료 단위, 진법 변환, 보수 및 음수 표현 (0) | 2023.04.27 |
| [논리회로] 종류 (0) | 2023.04.25 |
| [논리회로] 간소화 (0) | 2023.04.25 |



