■ 모델 행렬
먼저 모델 행렬(Model Matrix 혹은 World Transform Matrix라고 칭함)은 아래와 같이 구성되어있다.

위 T, R, S는 순서대로 이동(Translation), 회전(Rotation), 크기(Scale) 변환 행렬을 뜻한다. 위 조합으로 만들어낸 모델 행렬은 모델 공간에 위치한 정점들의 위치를 월드 좌표 기준의 위치로 변환해준다.
1. 크기 변환 행렬 (S)

2. 회전 변환 행렬 (R)

3. 이동 변환 행렬 (T)

위 세 개의 행렬들을 조합하여 나온 모델링 행렬은 아래와 같다.
4. 모델 행렬(M)

이를 토대로 코드를 구현해봤다. 원근투영행렬과 이동행렬은 전북대 교수님 강의를 따라 코드를 작성하며 이해를 한 뒤 다시 처음부터 제작해봤고 크기와 회전변환 행렬은 이전에 공부한 내용들을 토대로 스스로 구현해봤다.
외부 라이브러리인 glm을 설치 후 mat4, vec4와 같은 벡터, 행렬 클래스를 빌려 사용하였다.
그리고 제작 후에는 glm의 rotate 함수 등을 사용해봄으로써 직접 제작한 변환 행렬이 의도한바와 같이 행동하는지 비교하는 등 실험을 해봤었다.
[OpenGL]
1. 크기 변환 행렬

2. 회전 변환 행렬

이는 내가 이전에 공부했던 회전 변환 행렬의 이론을 토대로 제작해봤다. (이전 포스팅)
작동이 잘 되는 것을 확인했었으나, ChatGPT가 알려준 방식, glm의 라이브러리 속 Rotate 함수의 내용은 내가 했던 방식과 흡사하면서도 달랐다. 이에 대해서는 추후에 공부를 많이 해봐야겠다.
3. 이동 변환 행렬

먼저 이동 변환 행렬을 구현해봤다. mat4의 생성자에 행렬의 요소들을 넘겨줬었다. 하지만 glm의 Matrix는 열벡터를 기준으로 하기 때문에 이를 전치한 후에 사용할 필요가 있었다.
| 전치 이전에 이동변환 행렬의 모습 | 전치 이후에 이동변환 행렬의 모습 |
 |
 |
전치를 해줘야 비로소 우리가 원하는 이동 변환행렬이 나온다는 것을 알 수 있었다.
■ 원근 투영행렬
[이론]
먼저 화각(θ)과 초점 거리(d)의 관계를 이해해야 한다.

일단 투영평면의 위치는 위 아래 크기가 각각 1이 되는 지점으로 결정된다. 좌우, 상하가 [-1, 1]범위를 가지고있는 정사각형의 모습을 하고있으며 이 평면 위에 물체의 상이 맺히게 된다. 이러한 평면에 대응하는 정사각형 영역을 NDC(Normalized Device Coordinate)라고 부르고 이 NDC가 일정한 값을 가지려면 화각이 커질수록 초점거리는 가까워지고 화각이 작아질수록 초점 거리는 멀어지게 된다.
[예]
| 화각이 커졌을 때 | 화각이 작아졌을 때 |
 대충 그렸어가지고 빨간색의 길이가 길어보이는데.. 다른 사진들과 같은 길이를 갖고 있다고 생각하면된다. |
 |
여기서 초점거리 d는 주어진 화각에 따라 다음과 같이 구할 수 있다..

그리고 초점거리와 같이알아야 하는 것은 종횡비(Aspect Ratio)이다. NDC는 1:1 의 크기를 갖는 정사각형이지만, 우리 컴퓨터의 스크린은 1:1의 길이를 갖고 있지 않기 때문이다. 그러므로 물체를 올바르게 투영해주고 싶다면 가로세로비율에 맞게 변환해줘야한다. 이를 변수 a라고 하면 종횡비는 아래와 같다.
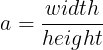
이를 갖고 동차좌표계(Homogenous Coordinate System)를 사용하여 한 차원 높은 행렬을 구한다면 아래의 모습을 갖는다.

위 행렬에 최종적으로, 근평면과 원평면을 활용한, 깊이값을 넣은 원근투영행렬은 아래와 같다.

[참고]
* n (near) = 카메라로부터 근평면까지의 거리
* f (far) = 카메라로부터 원평면까지의 거리
[OpenGL 코드]

■ 적용

위와 같이 모델행렬과 원근투영행렬을 구해줬다면
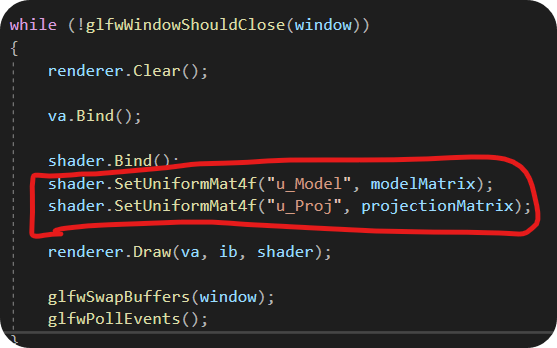
렌더링 하는 부분에서 쉐이더에 있는 uniform 변수에다 값을 설정해준다.

버텍스 쉐이더 부분이다. 버텍스의 Position인 벡터 값에다가 앞서 구한 모델 행렬과 투영 행렬을 곱해줬다.

앞서 설정한 크기 변환 행렬 (x축으로 2만큼 증가)이 적용된 모습이다.
아래는 회전 변환 행렬에 Roll 회전을 45도 한 결과이다.


아래는 이동 변환 행렬의 값을 변경 후 적용한 모습이다.


코드는 3차원 오브젝트 관련하여 작성하였지만 2차원 직사각형을 렌더링 하였기 때문에 다음에 3차원 오브젝트를 그려낼 때 Roll, Pitch, Yaw 세 가지 회전을 모두 이미지를 첨부할 예정이다.
'Computer Graphics > OpenGL' 카테고리의 다른 글
| [Computer Graphics] OpenGL, 더블 버퍼링 (0) | 2023.11.16 |
|---|---|
| [Computer Graphics] 공부 시작 및 목표 (0) | 2023.11.16 |

