■ 정의
자료구조란 계산에 쓰이는 여러가지 자료들을 조직화 및 구조화(organize)한 것을 의미한다.
■ 일상생활과의 비교
| 일상생활 | 자료구조 |
| 물건을 쌓아두는 것 | 스택 (LIFO; Last In First Out) |
| 영화관 매표소의 줄 | 큐 (FIFO; First In First Out) |
| 할 일 리스트 | 리스트 |
| 영어 사전 (알파벳 순서) |
사전, 탐색구조 |
| 지도 | 그래프 |
| 조직도 | 트리 |
■ SW코딩
[의미]
대부분의 SW코딩은 자료(data)를 처리하며, 이 자료들은 자료구조(data structure)를 사용하여 표현되고 저장된다. 이는 여러 가지 측면으로 SW코딩이 무엇인지를 나타낼 수 있다.
| 측면 | 정의 |
| 이론적 | 그래프이론, 집합이론, 조합적 분석의 이산수학과 확률이론을 기초로 알고리즘을 분석하여 검색, 정렬방법을 결정함. |
| 효율적 | 공간복잡도, 시간복잡도를 기초로 효율 분석을 하여 최적의 상태를 결정함. |
| 실제적 | 자료를 문자열, 리스트, 트리, 그래프, 파일 구조로 표현하고 알고리즘을 구현하고 SW코딩과 파일 작성, 메모리 관리, 운영체제 등에 적용함. |
[자료구조가 필요한 이유]
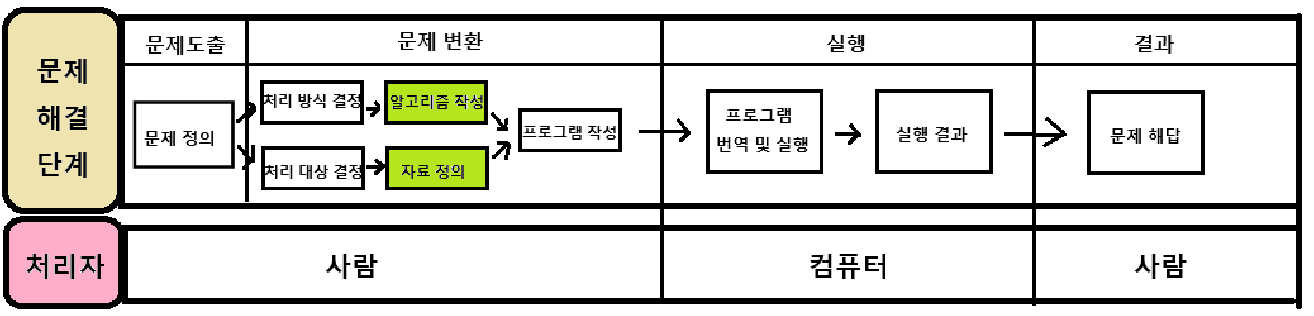
효율적으로 문제를 처리하기 위해선 문제를 정의하고 분석하여 최적의 설계를 작성해야 함. 이 과정에서는 아래와 같이 알고리즘과 자료구조가 사용이 되므로 프로그램을 제작할 때 자료구조의 지식이 꼭 필요하다는 것을 알 수 있음
■ 자료 형태에 따른 분류
(1) 단순 구조
자료값을 사용하기 위한 기본 형태. 코딩 언어에서 제공하는 정수, 실수, 문자, 문자열 등의 데이터 타입
(2) 비선형 구조
계층 구조나 망구조를 갖는 트리, 그래프 등의 자료구조
(1:n 혹은 n:n의 구조)
(3) 파일 구조
레코드 집합인 파일에 대한 자료구조. 보조기억장치에 데이터가 실제로 저장되는 형태. 순차파일, 색인파일, 직접파일 등이 있음.
(4) 선형 구조
자료들의 관계가 1:1 관계인 것. 순차리스트, 연결리스트, 스택, 큐, 데크 등이 있음.
| 종류 | 특징 |
| 순차리스트 | 자료의 논리적인 순서와 기억장소에 저장되는 물리적인 순서가 일치하는 구조 |
| 연결리스트 | 기억장소에 저장되는 물리적인 순서와 관계없이 포인터를 이용하여 논리적인 순서대로 연결하는 구조 |
| 스택, 큐, 데크 | 자료의 삽입이나 삭제 위치에 대한 제한조건이 있는 리스트 |
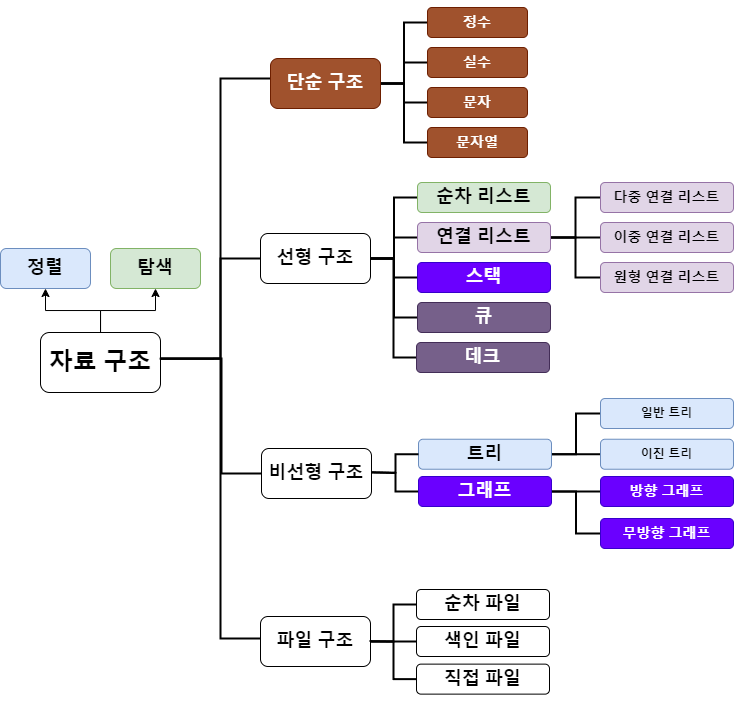
아래는 자료 형태에 따라 분류한 자료구조의 종류를 draw.io홈페이지를 이용하여 표현해봤다.
■ 컴퓨터에서의 자료 표현
컴퓨터에서 자료를 표현하는 방식은 여러 가지다.이에 대표적으로 몇 가지가 있는데 아래와 같다.
| 방식 | 데이터 단위 |
| 2진수 코드 | (1, 0) or (true/false) or (on/off) |
| 최소 단위 | 비트 (Bit) |
| 4비트 그룹 | 니블 (Nibble) |
| 8비트 그룹 | 바이트 (Byte) |
자료를 표현할 때, 보통 최소단위인 비트를 활용해서, n비트로 2^n개의 상태를 표시하여 자료를 표현한다.
위 방식으로 표현할 수 있는 자료의 종류는 아래와 같다.

■ 10진수 표현 : 존(Zone) 형식
10진수 한 자리를 표현하기 위해서 1Byte (8Bit)를 사용하는 형식.
| 요소 | 특징 |
| 존 영역 | · 상위 4비트 · 1111로 표현 |
| 수치 영역 | · 하위 4비트 · 표현하고자 하는 10진수. 한 자리 값에 대한 2진수 값을 표시. |
| [존 형식의 구조] | |
 1바이트 (8bit)를 존 영역과 수치 영역을 나눠 표현한 것. 10진수로 표현한 숫자의 한 자리를 표현하기 위해 위 만큼의 공간이 필요함. |
|
| 방법 |
| 2(1) 10진수의 자릿수만큼 존 형식을 연결하여 사용 (2) 마지막 자리의 존 영역에 부호를 표시. (양수면 1100, 음수면 1101)  (ex. +2133의 예. 만약에 -2133이라면 마지막 zone은 1101인 D가 되어야 한다) |
■ 10진수 표현 : 팩(Pack) 형식
위 Zone 형식은 한 자리의 숫자를 표현할 때마다 1111의 고정된 값을 가진 Zone 구간을 항상 붙여 표현해야한다. 이는 메모리 공간을 낭비하는 비효율적인 방식으로 실제 컴퓨터에서 10진수를 표현할 땐 Pack 방식을 이용한다.
| 방법 |
| (1) 존 영역은 항상 1111로 표시되므로 메모리를 낭비하므로 이를 제거한다. (2) 10진수 한 자리를 표현하기 위해서 존 영역 없이 4비트를 사용하여 표현한다. (3) 최하위 4비트에 부호를 표시한다. (양수면 1100, 음수면 1101) 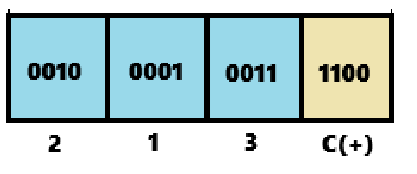 (ex. +213의 예. 만약에 -213이라면 마지막 4비트는 1101인 D가 되어야 한다) |
■ 2진수 표현 : 정수 (부호 절대값)
일정한 길이의 n비트로 표현한다. 부호와 절댓값 형식으로 표현하기에 부호절대값이라고 표현한다.
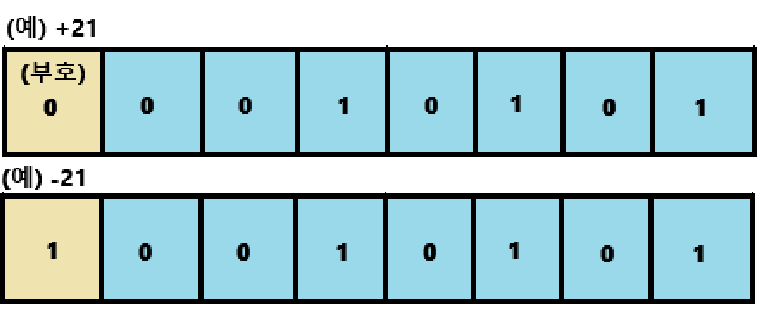
부호는 양수(0)와 음수(1)로 표현한다.
■ 2진수 표현 : 정수 (1의 보수)
보수(Complement)란 반대의 수를 의미한다.
1의 보수는 양수에서는 부호 절대값 형식을 그대로 따르고, 음수를 표현할 때 부호 비트를 사용하는 대신 1의 보수를 사용하는 방법이다.
| 방법 |
| n비트를 모두 1로 만든 이진수에서 변환하고자 하는 이진수를 뺌 (예) 10진수 21을 1의 보수로 만듦 (1바이트 사용) 1111111 - 00010101(-21의 절대값) = 11101010 (21의 1의 보수 = -21) 위 과정을 본다면 1의 보수를 구하는 과정은 XoR연산자를 통해 구해지는 것을 알 수 있다. XoR : 두 수가 같다면 0, 두 수가 다르다면 1을 반환한다. [계산 이후] MSB(최상위비트; Most Significant Bit)값은 부호를 나타내는 숫자이므로 나머지 7비트로 값을 표현하는 것을 감안해보자. [0][0010101]은 21이였고 [1][1101010]은 -21인 것을 알 수 있다. 이를 21의 1의 보수라고 칭한다. [추가 설명: 캐리가 있을 경우 (lhs > rhs)] 유도과정을 위해 예시로 '13-10=3' 계산식을 활용하겠다. (1) 13 = 1101, 10 = 1010 이다. (2) 10에 대한 1의 보수[-10]는 0101인 것을 우리가 알 수 있다. (3) 1101 + 0101 = 10010 이 나온다. (4) 4비트로 표현해야하는데 5비트가 나와버렸다. 이럴 때 최상위비트를 캐리[Carry]라고 하는데 이 캐리를 최하위 비트에 더해준다. (5) 과정4를 연산하면 0011, 즉, 3의 값이 나온다. [추가 설명: 캐리가 없을 경우 (lhs < rhs)] (1) 13 = 1101, 10 = 1010 이다. (2) 13에 대한 1의 보수[-13]는 0010인 것을 우리가 알 수 있다. (3) 1010 + 0010 = 1100 이 나온다. (4) 1100에 대한 1의 보수를 다시 한 번 진행시킨다. (5) 0011. 즉, 3이 나온다. |
■ 2진수 표현 : 정수 (2의 보수)
양수에서는 부호절대값 형식을 그대로 따르고, 음수의 표현에서 부호 비트를 사용하는 대신 2의 보수를 사용하는 방법.
| 방법 |
| 1의 보수에 1을 더함. (예) 10진수 21을 2의 보수로 만듦 (1바이트 사용) 11101010 (21의 1의 보수) 여기에 1을 더한 11101011이 21의 2의 보수가 된다. [추가 설명: 캐리가 있을 경우 (lhs > rhs)] 유도과정을 위해 예시로 '13-10=3' 계산식을 활용하겠다. (1) 13 = 1101, 10 = 1010 이다. (2) 10에 대한 2의 보수[-10]는 0110인 것을 우리가 알 수 있다. (3) 1101 + 0110 = 10011 이 나온다. (4) 캐리가 발생했다. 2의 보수에선 캐리가 발생하면 이를 버리게 되어있다. (5) 0011 = 3 이다. [추가 설명: 캐리가 있을 경우 (lhs < rhs)] (1) 13 = 1101, 10 = 1010 이다. (2) 13에 대한 2의 보수[-13]는 0011인 것을 우리가 알 수 있다. (3) 1010 + 0011 = 1101 이 나온다. 이는 십진법으로 13이 나와버린다. (4) 캐리가 발생하지 않았다. 1의 보수의 방식과 비슷하게 다시 한 번 더 2의 보수를 구해준다. (5) 1101에 대한 2의 보수는 0010 + 0001=> 0011인 것을 알 수 있다. |
■ 아니 1의 보수가 있는데 2의 보수는 왜 사용하는거지?
[설명]
4비트로 표현할 수 있는 숫자의 개수는 2^4 = 16개다. 맨 앞 비트는 부호를 위해 사용된다는 것을 기준으로 우리가 이진법으로 표현할 수 있는 숫자의 범위는 0000~1111이다. 여기서 주의할점은
0000 = +0, 1000 = -0의 값을 갖는다. 우리가 일상생활에서 0에 대해서 양수, 음수를 구분할 필요가 없음에도 불구하고 1의 보수는 +0과 -0에대한 각각의 보수값[0000, 1111]을 갖게되기 때문에 1비트를 낭비해버린다.
저장효율을 떨어뜨리는 이의 방법을 보완하기 위해 2의 보수가 생겨났다. 2의 보수는 발생한 캐리를 버리기 때문에
+0과 -0이 0000 같은 값이 되어버려 구분할 필요가 없어진다. 이렇게 1비트를 아낄 수 있기 때문에 기존의 범위[+0~+7, -0~-7]에서 [-1~-8, +0~+7]만큼 넓어지게 된다.
[요약]
(1) 부호비트 방식과 1의 보수표현법은 +0과 -0의 표현이 다르다. 그러나 2의 보수표현법은 +0과 -0의 표현이 하나로 같은 표현이다.
(2) 2의 보수는 +0, -0을 하나로 표현할 수 있어서 저장의 효율이 향상된다.
이러한 이유로 컴퓨터에선 실제로 2의 보수를 사용한다고 한다.
■ 2진수 표현 : 실수 (부동소수점)
십진법을 예로 9.625라는 숫자가 있다고 하자.
이를 이진법으로 표현하면 1001.101이다. 부동소수점은 모든 이진수를 1.xxx으로의 형식으로 변환한 숫자이다.
1001.101이 1.xxx형태로 변하려면 소수점이 왼쪽으로 세 칸 움직여야 한다.

부동소수점은 32비트를 기준으로 첫 비트(MSB)는 양수(0)와 음수(1)를 구분하는데 사용하고 그 다음 8비트를 소수점이 몇 칸 움직이일지를 나타낸다.
아까 위 예시를 기준으로 세 칸을 움직여야 우리가 원하는 1.xxxx형태로 변환할 수 있으므로 8비트가 최대로 나타낼 수 있는 숫자 127를 기준으로 130에 대해 뺄셈을 해줘야 3 [세칸 움직인다는 표시]이 나온다.
쉽게 말해 8비트를 활용하여 8비트의 최대수 127과의 차이를 움직일 칸의 개수를 나타낸다는 뜻이다.
그리고 나머지 23자리엔 소숫점이 움직인 결과에서 실수부분을 넣어주면된다.]
(ex. 9.625 = 1001.101, -> 1.001101 (floating point))
▼ 결과값
[0][1000001][00011010][00000000][00000000]
▼ 부동소수점에서 이진법 소수표현
1.001101 -> 130-127 = 3 칸움직임 -> 1001.101 (9.625)

(출처: 링크) <- 도움이 많이 되니 꼭 참고하길 바람
[부동소수점 두 가지 방식]
(1) 부호(1bit) + 지수(8bit) + 가수(23bit) = 32bit (단정도 방식). 우리가 흔히 쓰는 float타입이다.
(2) 부호(1bit) + 지수(11bit) + 가수(52bit) = 64bit (배정도 방식). 우리가 흔히 쓰는 double타입이다.
위 처럼 부동소수점을 표현하는 방식들은 IEEE[전기전자공학자협회]에서 규정한 IEEE754표준 방식이다.
'Computer Science > Data Structure' 카테고리의 다른 글
| [자료구조] 이진탐색트리 (Binary Search Tree) (0) | 2024.03.29 |
|---|---|
| [자료구조] 그래프 (Graph) (0) | 2024.03.25 |
| [자료구조] 우선 순위 큐 (Priority Queue) (0) | 2024.03.25 |
| [자료구조] 순환적, 반복적 피보나치 수열 구현 및 성능 비교, 순환문과 반복문 비교, 하노이탑 (0) | 2024.02.03 |



