■ 행렬의 덧셈
행렬의 덧셈은 A, B 행렬 모두 크기가 동일해야한다.

1+2, 7+8, 이런식으로 원소끼리 덧셈을 해주면 된다. 그러므로 열과 행의 길이가 같아야한다.
이 또한 모듈화를 위해 def로 함수로 만들었다 :)

■ 행렬의 뺄셈

■ 행렬의 스칼라 곱

행렬의 스칼라 곱은 행렬의 크기가 몇 배로 늘어나냐는 의미이다. 각 원소에 스칼라 값을 곱해주면된다.
■ 행렬의 원소 곱

행렬의 원소 곱은 두 행렬의 해당 인덱스에 위치한 원소끼리 곱해주는 것이다.
A와 B의 원소 곱을 예시로 수학적 표기는 아래와 같다.

가운데 ⊙ 표시는 원소끼리 곱하는 원소곱을 의미한다.
■ 행렬의 곱셈
행렬의 곱셈은 처음에는 약간 복잡하게 다가오는 개념이다.
하지만 계산을 계속 하다보면 매우매우 간단한 것을 깨닫게된다.
일단 행렬을 정의하자면 원소를 표준화해서 표시할 때 아래와 같이 표시한다.

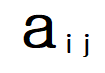
즉 a11은 1행 1열에 위치한 원소 라는 뜻이다.
이제 행렬의 곱셈을 보자.
행렬의 곱셈을 계산할려면 파라미터로 넘겨지는 두 행렬은 아래 조건을 충족시켜야한다.

위 예시를 기준으로 A는 3x2사이즈이고 B는 2x3 사이즈이다. 첫번째 인자의 열 벡터 크기와 두번째 인자의 행 벡터 크기가 동일해야한다.
하지만 곱셈을 한다면 아래와 같은 결과가 나온다.

아래 A, B를 예시로 하자면


이 방향대로 계산을 한다고 생각하면된다. AB가 바뀌었을 때도 첫번째 인자(B)는 행(row) 방향으로 계산한다고 생각하면된다.
위 AB를 기준으로 설명하자면 먼저 결과값으로 나오는 행렬은 3x3 사이즈로 나올 것이다.
[0][0]번째 원소는 (A[0][0] * B[0][0]) + (A[0][1] * B[1][0]) 값이 들어간다.
즉 A11과 B11을 곱한 값과 A12과 B21를 곱한 값을 더하면 되는 것인데 A는 위 화살표대로 행 방향으로 인덱스가 움직이고
B는 열방향으로 인덱스가 움직인다.
그리고 결과값이 들어갈 원소 인덱스 자리는 각각 A의 행과 B의 열을 기준이 되는 인덱스가 된다.

이를 파이썬으로 구현해봤다.


■ 모듈화 (커스텀 라이브러리)



위 행렬곱도 실제 계산해서 검증해봤다

■ 행렬의 대각합
대각합(Trace)이란 행렬 A가 정사각행렬일때 주 대각 원소를 모두 더한 값을 의미한다.
* 주 대각 원소란 행렬의 행 번호와 열 번호가 동일한 원소를 뜻한다.
대각합의 수학 기호는 tr(A)가 된다.




■ 행렬의 덧셈 (넘파이)

■ 행렬의 뺄셈 (넘파이)

■ 행렬의 원소곱 (넘파이)

■ 행렬의 스칼라곱 (넘파이)

■ 행렬의 곱 (넘파이)

'개발 (AI) > 선형대수' 카테고리의 다른 글
| [행렬] 대각 행렬 (0) | 2023.05.07 |
|---|---|
| [행렬] 대칭 행렬 (0) | 2023.05.06 |
| [행렬] 전치행렬 (0) | 2023.05.06 |
| [행렬] 공부할 행렬 종류 (0) | 2023.05.06 |
| [행렬] 스칼라, 벡터 (0) | 2023.04.28 |


