■ 개념 및 배경
선 그리기 알고리즘 (line algorithm)의 대표 모델이다.
우리가 원하는 물체를 컴퓨터 스크린 화면에 나타내는 작업을 픽셀화(Rasterization)라고 한다. 데카르트 좌표계 위에 존재하는 벡터들을 스크린 좌표계로 옮겨주는 작업인데 이때 신경써야할 점들이 존재한다.
| 이름 | 데카르트 좌표계 (Cartesian coordinate) |
스크린 좌표계 (Screen coordinate) |
| 집합 | 실수 집합 (R) | 양수 집합 (H) |
| 성질 | 연속성 | 이산성 |
| 원소 | 벡터 | 픽셀 |
| 예시 그림 |  우리가 수학에서 일반적으로 사용하는 좌표계이다. 연속성을 가지고 있으며 무한한 실수로 이루어져 있다. |
 서로 독립된 픽셀 영역을 가진 스크린 좌표계이다. 0부터 시작하는 정수값을 가지고 데카르트 좌표계의 좌표를 스크린 좌표계로 변환하여 표현하고싶다면 실수로 구성된 벡터좌표 (x, y)를 정수로 변환해야한다. |
■ 원리
위와 같은 차이로 무한한 실수의 집합인 데카르트 좌표계에 존재하는 벡터들을 이산성을 띄고있는 스크린 좌표계에 표현할려면 어떻게 해야할까?
먼저 아핀공간에서 직선을 그리는 방정식은 아래와 같다. (이건 추후 시간되면 정리글 올릴까 생각중)
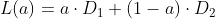
위 식에서 스칼라 a값의 범위 [0, 1]에 해당하는 수많은 벡터를 생성하고 이에 대응하는 픽셀을 촘촘히 찍어서 하나의 선을 보여주는 방식을 택해야하는데 이렇게 된다면 컴퓨터가 선 하나 그리는 것만 해도 과부하에 걸릴 것이다.
위와 같은 상황에서 최적화된 방식으로 선을 그리기 위해 고안된 것이 '브레젠험 알고리즘'이다. 정수형 연산만을 사용해서 선을 그리는 알고리즘이다.

위와 같이 점1와 점2가 정해지면 선분(Segment)이 그려진다. 선분이 지나는 자리에는 픽셀들이 위치해있는데 예시 속에서도 볼 수 있듯이 픽셀 두개를 동시에 지나는 경우가 있다. 그런 경우 둘 중 하나를 골라줘야하는데 두 픽셀을 지나는 가운데를 기준으로 노란색 선이 더 짧다면 아랫부분을 초록색이 더 짧다면 위에 존재하는 픽셀을 골라주는 방식이다.
그러면 둘 중 어느 것이 더 가까운지 어떻게 알까? 스크린 좌표계를 8등분한 것을 표현한 화면이다.

대표적인 예로 1팔분면 (x축 끊임없이 증가, y축은 평행 or 감소)에 대해 확인해보면 아래와 같다.

선분이 지나는 두 픽셀의 가운데를 기점으로 오른쪽으로 평행이동 할지 혹은 y축을 감소시킬지 정하게 되는데 해당 판별식은 아래와 같다.

이를 간단히 표현한다면 아래와 같다.

h는 y의 변화량 (진행방향) w는 x의 변화량 (진행방향)이다. height와 width의 줄임말로 h, w를 사용했다.
이는 흔히 알고있는 직선의 방정식에서 유도된다.

위 방정식을 갖고 (x0, y0)에서 시작한다고 했을 때 다음 픽셀을 위한 판별식은 아래와 같이 구해진다.


위 b를 다시 직선의 방정식에 대입하면

위와 같은 방정식을 구할 수 있다. 이 수식의 Y값을 중점으로 y0 + 0.5와 비교하는 부등식을 만들어낼 수 있다.

y값이 Y0+0.5보다 작으면 수평으로 이동하고 아니라면 한 칸 아래로 내려가서 픽셀을 찍는다. 이 식을 단순화하겠다.






이를 맨 처음과 같이 '2h-w < 0'로 간편화 해준다면 보기에도 간단하고 높이와 너비만으로 다음 픽셀의 위치를 구할 수 있게되었다.


그러면 다음 픽셀의 위치는 각 픽셀들의 판별식을 활용하여 구해주면 될것이다.
| 2h-w에서 한칸 내려가면 2h-3w이 되는 이유 |
 위 부등식 우변에 위치한 ΔxY0 + Δx0.5 부분에서 다음 y의 위치값은 ΔxY0 + Δx1.5가 되는데 차후 2를 곱하는 부분에서 Δx3이 되기에 3w가 되는 것이다. |
(영상 참고)
https://www.youtube.com/watch?v=RGB-wlatStc&t=1979s
유니티 실습은 다음 글에 올릴 예정
[도서 참고]
이득우의 게임 수학 | 이득우 - 교보문고
이득우의 게임 수학 | 39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했
'Computer Graphics > Math' 카테고리의 다른 글
| [Math] 외적, 백페이스 컬링, 로드리게스 회전 (3) | 2023.12.18 |
|---|---|
| [Math] 3D 회전행렬 (1) | 2023.12.12 |
| [Math] 브레젠험 알고리즘 with Unity (0) | 2023.12.09 |
| [Math] 내적, 램버트 반사, 시야각 판별 (1) | 2023.12.06 |
| [Math] 삼각함수 (1) | 2023.12.03 |



