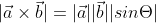■ 외적
내적 같은 경우 서로 같은 위치에 있는 요소끼리 연산을 하지만, 외적은 서로 다른 위치에 존재하는 요소만 사용한다.
예로 외적의 계산은 아래와 같다.
[공식]
아래와 같이 벡터u와 벡터v가 있다고하자. 내적은 · 기호를 사용했디면, 외적에선 x 기호를 사용한다.


처음에는 위 수식이 어려워보였으나, 앞서 회전행렬을 공부하면서 회전의 순환 순서가 x->y->z->x->y->z...라는 것을 생각하면 조금 친숙해보일 것이다.
(1) x요소 : UyVz - VyUz, 이를 보면 x축을 제외한 yz순서대로 Uy와 Vz를 곱한 값에 Vy와 Uz를 곱한 값을 감소시킨다.
(2) y요소 : UzVx - VzUx, 이를 보면 y축을 제외하고 회전 순환 순서대로 zx순으로 연산하는 것을 알 수 있다.
(3) z요소 : UxVy - VxUy, 이를 보면 z축을 제외한 xy 순서대로 연산하는 것을 볼 수 있다.
[내적과의 차이]
| 내적 (Dot Product) |
외적 (Cross Product) |
|
| 반환값 | 스칼라(Scalar) | 벡터(Vector) |
| 교환법칙 | O | X |
| 결합법칙 | X | X |
| 분배법칙 | O | O |
| 삼각함수 관계 | 벡터의 내적은 사잇각 cosθ에 비례 |
벡터 외적의 크기는 sinθ에 비례 |
| 응용 | (1) 앞 뒤 판별 (2) 시야각 내 물체 판별 (3) 조명 효과 (램버트반사) (4) 투영벡터 |
(1) 평행성 판별 (2) 좌우 판별 (3) 평면의 법선벡터 생성 (백스페이스 컬링에 활용한다.) |
■ 백페이스 컬링
백페이스 컬링(Backface Culling)이란 물체를 렌더링할 때 메시를 구성하는 삼각형의 면의 방향을 판별해 카메라와 같은 방향을 쳐다보고있으면, 삼각형의 뒷면을 모니터에 띄워줘야하는 것이기 때문에, 해당 면을 컬링해서 렌더링하지 않는 기법이다. 즉, 우리가 앞면을 볼 수 있는 삼각형만 골라서 렌더링 해주는 기술이다.
같이 공부하고 있는 OpenGL은 오른손 좌표계를 사용한다. 그러므로 오른손을 기준으로 예시를 그려봤다.
[예시]
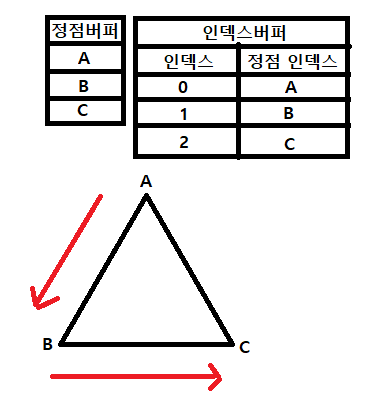
위와 같이 인덱스 버퍼를 봤을 때 A -> B -> C 순으로 그리는 것을 알 수 있는데 이는 오른손의 엄지가 위로 향한 상태에서 손을 움켰을 때 손가락이 감기는 방향과 동일한 것을 알 수 있다.



위를 통해 B-A인 벡터 u와 C-A인 벡터 v의 외적은 엄지손가락 방향대로 위로 향하는 벡터가 만들어진 다는 것을 알게되었다. 그러면 위와 같은 방향으로 만들어진 삼각형은 앞면이 위로 향하는 삼각형이라는 것인데 백스페이스 컬링에선 이와 같은 방향을 가진 삼각형만 렌더링 해준다.
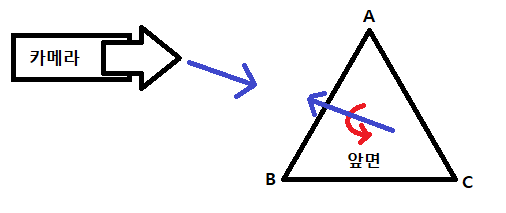
만약 인덱스 버퍼 내 정점을 그려주는 순서가 A-C-B였다면? 엄지손가락이 아래로 향하는 것을 알 수 있다.


그러면 벡터u와 벡터v를 외적한 결과로 스팬한(Spanned) 벡터는 아래로 향한다는 것을 알 수 있다.
그렇다면 우리가 카메라로 쳐다보는 것은 삼각형의 뒷면인데, 백페이스 컬링은 위 예시와 같이 카메라와 같은 방향을 쳐다보는 삼각형들을 컬링해주는 기법인 것이다.
[효과]
이는 그래픽스에서 최적화를 위해 많이 사용하는 기법이다. 예로 정육면체의 상자를 하나 그린다고 할때 6개의 면을 다 그려준다면 100개의 상자를 그릴 때 총 600개의 면을 그려줘야한다. 하지만 백페이스 컬링을 한다면 하나의 상자에 3개의 면만 보여주면 되기 때문에 렌더링 해줘야하는 면의 개수가 반이나 줄어들게 된다.
■ 로드리게스 회전
이전 포스팅에서 3차원 공간에서의 회전과 관련된 행렬을 다뤘었다. 오일러각을 활용해 회전을 하는 과정을 유도해봤었는데 이는 회전 보간이 어려울 뿐더러 짐벌락(Gimbal-lock) 현상이 발생한다는 취약점이 있다. 이 문제는 크게 두 가지로 해결이 가능한데 축-각 회전(Axis-Angle Rotation) 방식을 활용하거나 사원수를 이용한 회전을 구하면 해결할 수 있다.
로드리게스 회전은 위 축-각 회전을 활용한 방식으로 3차원 공간에서 임의의 축을 골라 이에 직교하는 평면에 회전을 진행시키는 형태를 띠고있다.
[내적과 외적을 활용한 유도 과정]

현재 정점의 위치 P와 회전축 A 그리고 얼만큼 회전할지의 정보를 가진 θ(쎄타)를 가지고 회전 이후 P의 위치인 P'를 구할 수 있다. 그리고 가시적으로 계산하기 위해 원점을 O라고 하고 회전 평면의 중심점을 O'이라고 부르겠다.

원점O에서 O'으로 향하는 벡터는 벡터V이고, P-O는 벡터 u이다. 벡터 v는 크기가 1인 법선벡터(Normal Vector) n(hat)과 벡터u를 이용하여 투영벡터 공식을 대입해서 구할 것이다.
이를 통하여 공간의 원점인 O에서 회전 평면의 원점인 O'으로 향하는 벡터 V를 구할 수 있게 된다.

또한 우리가 회전이후의 정점의 위치를 알기 위해서는 선분 OP의 길이를 알아야한다. 이는 아래와 같이 구할 수 있다.

현재 까지의 모습을 2차원 평면으로 나타내면 아래와 같다.

아래와 같이 선분 O'P'은 반지름 r이 될 것이고 O'에서 P'의x까지의 길이는 x로 두어 직각 삼각형으로 만들어준다면 아래 계산 과정을 통해 P'의 x좌표를 구할 수 있다.

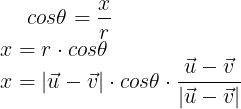
반지름 r의은 (벡터 u - 벡터 v)의 크기와 같으니 노름(Norm) 벡터 u - 벡터 v로 치환해주고
단위 벡터가 필요하기에 끝에 단위벡터를 구하는 식을 추가해줬다.
위 식을 간단히하면 아래와 같이 나온다
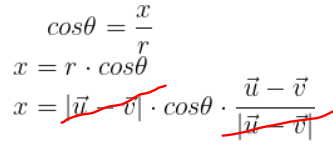

이제 P'의 y좌표만 구해주면 된다.
p에서 p'으로 향하는, y에 해당하는, 벡터를 구해주려면 외적을 사용해야한다.

회전축 A의 단위벡터 n.hat와 선분 O'P를 외적하면 선분 PP'와 평행하는 벡터를 구할 수 있게 되므로 아래의 공식을 이용할 수 있다.

그리고 선분 O'P'의 크기는 선분 O'P (벡터u-벡터v)의 크기와 같으며 유도과정은 아래와 같다.

이를 기억하고 다시 평면으로 돌아와서 보면 y를 구하기 위해 아래와 같은 과정을 겪어야 한다.


위 식에서 아래와 같이 정리된다.
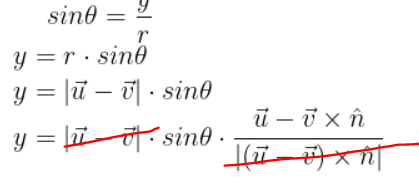

최종적으로 구한 P'의 x, y는 아래와 같다.
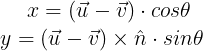
위 x, y를 통해 벡터 O'P를 θ만큼 회전한 벡터 O'P'은 아래와 같이 구할 수 있다.

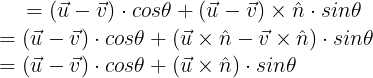
분배법칙 이후 벡터v x n.hat이 소거된 이유는 둘이 같은 방향을 바라보고있는 평행성을 갖고있기 때문이다. 평행성을 가진 두 벡터끼리는 외적 시 영벡터가 나오기 때문에 소거해줬다.
또한 위 식에서 마지막으로 벡터V를 더해줘야한다. 그 이유는
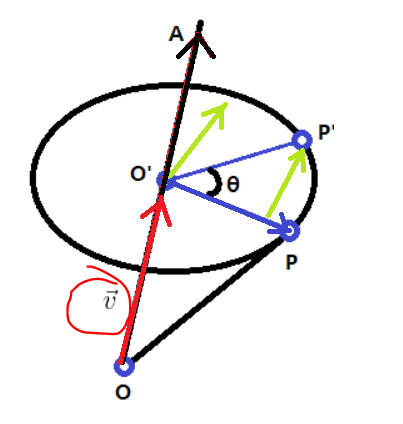
위와 같이 회전평면이 원점으로부터 벡터v만큼 떨어져 있기 때문이다.
이제 최종적으로 식을 정리하고 벡터 OP'을 구하자면 아래와 같이 된다.
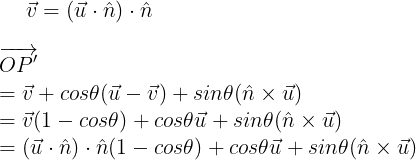
▼ 최종적으로 구한 로드리게스 공식
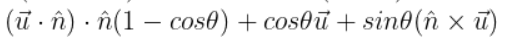
위 공식을 이용하면 오일러 각으로 표현하기 어려운 임의의 축에 대한 회전을 수행할 수 있다. 하지만, 행렬로의 변환이 까다롭기 때문에 게임 엔진에서는 로드리게스 회전보다는 간결하고 행렬 변환이 용이한 사원수를 사용한다.
[참고]
이득우의 게임 수학 | 이득우 - 교보문고
이득우의 게임 수학 | 39가지 실시간 렌더링 게임 프로그래밍 실습 예제를 하나씩 따라 해보며 독자가 직접 체득하는 흥미로운 게임 수학의 세계! 게임 개발자와 그래픽 아티스트들이 궁금해 했
'Computer Graphics > Math' 카테고리의 다른 글
| [Math] 비판정법, 매클로린 급수, 오일러 공식 (0) | 2023.12.31 |
|---|---|
| [Math] 3D 회전행렬 (1) | 2023.12.12 |
| [Math] 브레젠험 알고리즘 with Unity (0) | 2023.12.09 |
| [Math] 브레젠험 알고리즘 (Bresenham's algorithm) (0) | 2023.12.07 |
| [Math] 내적, 램버트 반사, 시야각 판별 (1) | 2023.12.06 |