■ 개념
이전에 배운 대각 행렬은 주 대각 원소들을 제외한 나머지 원소들이 0인 행렬인 것을 기억할 수 있다.
이중 대각 행렬(Bidiagonal Matrix)은 대각 행렬의 대각 원소의 위 혹은 아래쪽 원소들이 0이 아닌 행렬이다. 종류는 두 가지로 나뉜다.
■ 종류
(1) 상이중대각행렬 (Upper Bidiagonal Matrix)
이름 그대로 주 대각 원소의 바로 위 원소들이 0이 아닌 행렬이다. 한글 표기는 잘 안쓴다고 한다.

(2) 하이중대각행렬 (Lower Bidiagonal Matrix)
주 대각 원소 및 그 아래 원소들이 0이 아닌 행렬.

■ 파이썬
교재에서 파이썬 실습을 하기 전에 미리 어떻게 코드를 작성해야할지 고민을 해봤다. 규칙성을 찾기 위해
아래에 위치한 0, 위에 위치한 0들을 기준으로 분석해봤다..

간단한 행렬을 그려놓고 고민해봤다. 그 결과 Upper Bidiagonal Matrix, Lower Bidiagonal Matrix 둘 다 각각 다른 두 개의 규칙을 갖고 있는 것을 확인해봤다.
(1) 상이중대각행렬의 윗 부분 0들은 j-i가 1보다 큰 경우, 아래 부분 0들은 i가 j보다 큰 경우
(2) 하이중대각행렬의 윗 부분 0들은 i-j가 1보다 큰 경우, 아래 부분 0들은 j가 i보다 큰 경우
코드로 옮겨봤다.


▼ 반환된 행렬들을 나열해봤다

책의 코드와도 비슷했다.
■ 넘파이
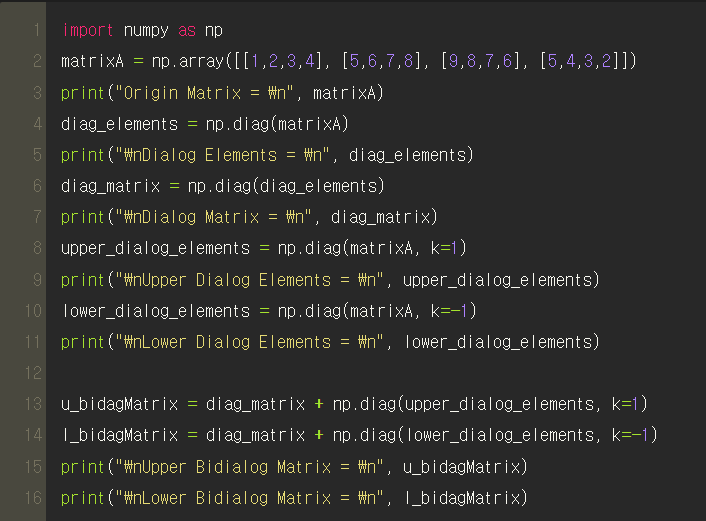

여기서 넘파이에 대해 더 배웠다.
(1) numpy.diag(리스트, k=n) 에서 두번째인자에 k=1, k=-1 등의 인자가 주어진다면 해당 리스트가 주 대각 원소에서 몇 번째 위로(양수) 혹은 아래(음수)로 위치시킨 행렬을 반환해준다. 예를들어 np.diag(elements, k = 1) 코드는 elements를 가운데로부터 위로 1 만큼 떨어진 대각 원소로 위치시킨 행렬을 반환해준다.
(2) numpy.diag(행렬, k=n) 은 반대로, 리스트로 반환해주되 주 대각 원소로부터 k만큼 떨어진 대각 원소를 반환해준다.
'개발 (AI) > 선형대수' 카테고리의 다른 글
| [행렬] 하우스홀더행렬 (0) | 2023.05.29 |
|---|---|
| [행렬] 토플리츠행렬 (0) | 2023.05.28 |
| [행렬] 삼각행렬 (0) | 2023.05.28 |
| [행렬] 영 행렬 (0) | 2023.05.07 |
| [행렬] 단위 행렬 (0) | 2023.05.07 |



